Comprendre (un peu) l'Intelligence Artificielle : la retro-propagation -> activité en classe

JTS décrira une astucieuse manière de mettre en œuvre, avec des boites d’allumettes et des billes colorées, un des mécanismes centraux de l’IA, la rétro-propagation d’erreur (on devrait plutôt dire rétro-propagation de correction d’erreur). Si le système n’a pas « fait juste » il se modifie pour ne pas refaire la même erreur, puis il se modifie pour ne pas refaire ce qui l’a conduit dans la configuration qui l’a mené à cette erreur. Cette activité pourrait aider les élèves plus jeunes ou moins portés sur l’abstraction. Martin Gardner (1971) l’applique à un jeu très simple qu’il nomme jeu d’hexapion (HER). JTS reprend ici sa description détaillée du mécanisme avec les boites d’allumettes.

Ensuite JTS évoquera une implémentation logicielle de ce jeu-là sur un ordinateur en 1972-73.
Puis JTS présenter une implémentation un peu plus ambitieuse d’un autre jeu, avec un dé et un total-cible à atteindre, qui a été nommé Talusumma. Sans développer l’algorithme, des éléments du fonctionnement seront évoqués, qui pourraient permettre d’aider les élèves moins portés sur l’abstraction à l’implémenter.
Faute de patience pour éduquer le logiciel, des stratégies d’apprentissage automatique avaient été développés et une comparaison de leurs performances sera présentée. (Réalisée par un collégien de 17 ans qui avait été lauréat au concours la Science Appelle les jeunes en 1975).
La qualité de l’apprentissage est encore un question délicate en IA et chercher la meilleure pourrait constituer un joli challenge pour des élèves en cours d’informatique.
Le code source (en FORTRAN pour HER, et BASIC pour Talusumma est mis à disposition sur demande pour des enseignants. N’étant pas devenu informaticien, et l’inspiration dans les documents de Martin Gardner n’utilisant pas les termes actuels comme algorithme, informatique, IA, qui n’existaient peut-être pas à l’époque, le lecteur plus compétent saura corriger d’éventuelles imprécisions de formulation.

Un des concepts de l’IA : la rétro-propagation

Une Illustration de la rétro-propagation en 1971

Martin Gardner explique l’origine de l’algorithme (sans utiliser ce terme, ni parler de retropropagation).  « Si certains lecteurs veulent expérimenter des machines perfectibles programmées pour certains jeux, il ne leur faudra pas nécessairement acheter un ordinateur. Il leur suffira de se procurer quelques boîtes d’allumettes vides et des perles colorées. Cette façon de réaliser une machine perfectible simple est une bonne invention de Donald Michie, un biologiste de l’Université d’Edimbourg […]. Il décrit une machine à jouer au tictactoe qu’il appelle MENACE (Matchbox Educable Naughts And Crosses Engine = Machine éducable à base de boîtes d’allumettes et de riens) ; il la réalisait à l’aide de trois cents boîtes d’allumettes. Gardner développe cet exemple en détail dans son texte encourage le lecteur à aller vérifier dans le texte d’origine :  ici

Une application concrète sans ordinateur : HER

Alors que les écoles doivent parfois enseigner l’algorithmique sans ordinateur, cet article donne une magnifique implémentation qui pourrait aider les élèves pour lesquels l’abstraction d’un algorithme est difficile.
Martin Gardner continue : « Comme il y a peu de chances que mes lecteurs puissent construire une machine utilisant trois cents boîtes d’allumettes, j’ai inventé le jeu d’hexapion. Il est beaucoup plus simple et la machine perfectible correspondante ne demande que vingt-quatre boîtes d’allumettes. Il est facile et sans gloire d’en faire l’analyse détaillée, mais je demande instamment à mes lecteurs de ne pas faire cette analyse. Il est beaucoup plus intéressant de réaliser la machine et d’apprendre à jouer en même temps qu’elle.

HER, le jeu d’hexapion

Le jeu d’hexapion se jouera sur neuf cases d’échiquier formant un carré de 3 x 3 ; trois pions occuperont les côtés opposés comme le montre la figure 2. On peut tout aussi bien utiliser des pièces de monnaie de diverses valeurs que de véritables pions d’un jeu d’échecs. Deux types de mouvement seulement sont permis : 1) un pion peut avancer droit devant lui d’une case si cette case est libre ; 2) un pion peut capturer un pion ennemi en passant en diagonale de sa propre case à une case occupée sur sa droite ou sur sa gauche. La pièce capturée est retirée du jeu. Ces mouvements sont ceux des pions au jeu d’échecs à l’exception du double coup initial, de la capture en passant et de la promotion pour obtenir une reine. »

Fig 1 :  Le jeu d’hexapion.[img]. Source :Gardner, M. (1971)

Pour gagner, il faut au choix :
1. Avancer un pion jusqu’à la troisième rangée.
2. Capturer tous les pions ennemis.
3. Bloquer l’ennemi sur une position qui ne lui permette plus aucun mouvement.
Les joueurs jouent chacun à leur tour en déplaçant une seule pièce à la fois. Il est évident que le match nul est impossible mais il n’apparaît pas à première vue qui du premier ou du second joueur aura l’avantage. »

Une implémentation avec des allumettes

Martin Gardner décrit ensuite ce que nous appellerons ici l’algorithme « Pour construire HER (Hexapawn Educable Robot = Robot éducable de l’hexapion), il suffit de vingt-quatre boîtes d’allumettes et d’un assortiment de perles colorées. […] Chaque boîte d’allumettes portera l’une des configurations de la fig. 2. Le robot jouera toujours en second. Les configurations notées « 2 » représentent les deux positions qui s’offrent à HER au second coup. On peut effectivement choisir entre l’ouverture centrale et l’ouverture latérale ; seule l’ouverture latérale gauche est figurée ; il est évident qu’on pourrait tout aussi bien la faire à droite mais la configuration obtenue serait l’image de la première dans un miroir. Les configurations notées « 4 » sont celles qui peuvent se présenter à HER à son second coup (le quatrième de la partie) : il y en a onze. Les onze dernières configurations notées « 6 » s’offrent à HER à son dernier coup (le sixième de la partie). On notera que parmi ces onze dernières configurations, certaines sont images l’une de l’autre ; c’est pour simplifier le raisonnement ; en les supprimant, dix-neuf boîtes suffiraient.
A l’intérieur de chaque boîte, on placera une seule perle colorée par type de flèches de la position correspondante. Le robot est prêt à fonctionner. Tout mouvement permis est représenté par une flèche ; le robot peut donc faire tous ces mouvements, mais seulement ceux-là. Il n’a pas de stratégie préétablie. On peut admettre qu’il est idiot.
Il s’éduque selon le processus suivant. L’homme qui lui sert d’adversaire fait l’ouverture. Il choisit ensuite la boîte qui porte la position ainsi réalisée, la secoue en fermant les yeux, ouvre le tiroir et retire une perle. Il referme le tiroir, pose la boîte en plaçant la perle retirée sur le dessus. Il ouvre alors les yeux, note la couleur de la perle, cherche la flèche correspondante et joue le coup ainsi déterminé. Il joue ensuite le troisième coup comme il le veut. Le même mécanisme se poursuit jusqu’à la fin de la partie. Si le robot gagne, replacer toutes les perles dans les tiroirs. S’il perd, le punir en confisquant la perle correspondant à son dernier coup. Replacer les autres perles et passer à la partie suivante. Si on tombe sur une boîte vide, ce qui est rare, il faut en déduire que la machine n’a aucun mouvement qui ne lui soit fatal et qu’elle se résigne. Dans ce cas, on confisquera la perle correspondant à l’avant-dernier coup.
[…] Après trente-six parties, dont onze défaites pour le robot, il a appris à appliquer une stratégie parfaite. Le système de punition préconisé permet de minimiser le temps nécessaire à l’éducation de la machine, mais il varie également en fonction de l’habileté de l’adversaire qui lui est opposé. Le robot se formera d’autant plus vite que son adversaire sera meilleur.

Fig 2:  Les configurations à dessiner sur les boîtes d’allumettes de HER. (Les quatre types de flèche (gras. tirets. etc) représentent quatre couleurs différentes des perles.).[img]. Source: Gardner, M. (1971)

En vidéo:

Pour aller plus loin, se faire plaisir ou pour des élèves motivés ?

Un algorithme implémenté vers 1973 en FORTRAN

L’algorithme pour HER décrit par Martin Gardner dans des textes proposés par son prof. de mathématiques, Bernard Louis, avait été implémenté par votre serviteur en langage FORTRAN.  Le code source est disponible  pour des enseignants qui voudraient s’en inspirer.  (Faute de lecteur de bandes perforées et cassettes magnétiques, seul le listing papier est encore utilisable de nos jours)

Une implémentation plus ambitieuse en 1975 sur un ordinateur à 4kHz avec 16 kb de mémoire :-))

Les limites d’un apprentissage avec les boites d’allumettes sont – entre autres – le nombre de situations possibles, les risques de fausses manipulations, de geste malencontreux, etc.  Mais surtout, il est vite apparu que le nombre de parties nécessaires à l’apprentissage, rebute la patience des joueurs humains.
Votre serviteur a choisi un jeu un peu plus intéressant, aussi proposé ailleurs par Gardner (1964) et simplifié du classique  « saut de la mort » .

Gardner décrit le jeu  « on joue avec un seul dé. On prend un nombre quelconque [le total cible], d’ordinaire supérieur à 20 pour rendre le jeu intéressant. Le premier joueur jette le dé, et marque le chiffre qui sort. Le second joueur fait basculer le dé d’un quart de tour de l’une quelconque des quatre manières possibles, et ajoute le chiffre qu’il amène au précédent. Les [2] joueurs se succèdent en faisant chaque fois basculer le dé d’un quart de tour et en additionnant successivement les chiffres sortants, jusqu’à ce que l’un d’eux gagne, soit qu’il atteigne le nombre fixé d’avance, soit que le joueur suivant le dépasse. »
Par exemple avec un total cible de 27, dans la situation de jeu suivante : total 26 et le 1 est en-dessous du dé, le joueur n’a pas d’autre choix que ce « saut de la mort ». (Gardner, 1964 p. 33).
Gardner n’ayant pas nommé ce jeu, le nom de Talusumma avait été retenu (Talus = dé en latin).

Stratégies et probabilité de victoire

Selon le total choisi, les chances de gagner sont – si on ne fait aucune erreur – de 50% (total cible 25) à 100% (total cible 27) pour le premier à jouer après le jeté initial du dé.
Selon Gardner (1964 p. 33), Il y a une stratégie qui assure la victoire… Saurez-vous trouver cette stratégie ? Ou laisserez-vous le logiciel la révéler à force de jouer ?

Quelques pistes pour la programmation :

Le jeu est défini, tout coup qui n’est pas gagnant est perdant. Ce cas est plus simple, puisqu’un coup qui a conduit à perdre la partie peut être éliminé de manière certaine. C’est une condition sine qua non pour ce type d’apprentissage qu’on nomme « par punition ». Il est intéressant de conséquent que dans ce cas le système n »apprend » que quand il perd, grâce à une stratégie d’apprentissage adaptée de ce que Gardner proposait.
Cela correspond finalement bien à l’apprentissage scolaire où l’élève n’ apprend de ses erreurs qui si on aide l’aide à les dépasser (feed-back formatif) pour aller vers la réussite (Brookhart, et al., 2008).

Pour Talusumma, la situations du jeu à un moment donné a été définie par le total courant, et le nombre affiché par le dé à ce moment de la partie (et évidemment le nombre à atteindre). Par exemple (total-cible=27;total actuel= 26;valeur affichée sur le dé = 1).
Il faut enregistrer le parcours (les situations et les coups joués) pour pouvoir faire la rétro-propagation : éliminer les coups perdants, et ceux qui y conduisent.
Comme on doit tourner le dé d’un quart de tour ni plus ni moins, le chiffre affiché et celui dessous sont exclus. Les possibilités de « coup » sont donc les chiffres de 1 à 6 sauf ces deux là. sauf le chiffre. NB: La  somme des faces sur les faces opposées est 7, donc le nombre au-dessous vaut 7 nombre au dessus du dé.
Dans l’exemple indiqué (total-cible=27;total actuel= 26;valeur affichée sur le dé = 1) le joueur (disons A) qui doit jouer dans cette situation_n a perdu (il ne lui reste que le saut de la mort ). Donc le coup précédent_n-1 de A qui a permis à B de jouer 1 et conduire A à cette situation_n perdante doit être éliminé. Si il ne reste alors plus de choix possibles (plus de billes) dans la situation précédente_n-1 on retire dans la situation_n-2 le choix qui a conduit A. On parcourt donc les choix de A en arrière jusqu’à tomber sur une situation où il reste des choix possibles (Retro-propagation).

Un challenge : trouver des stratégies pour éduquer le programme.

Vu le nombre de parties nécessaires à l’apprentissage, il est vite apparu à ce collégien en 75 qu’il fallait trouver des stratégies logicielles pour éduquer le programme.

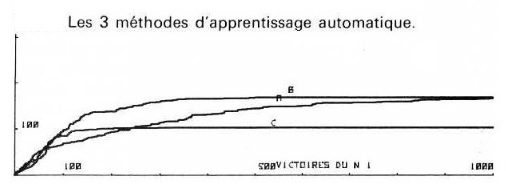
A l’époque trois stratégies ont été testées… la première, contre un générateur aléatoire,  n’avait pas encore terminé un apprentissage complet en une nuit de calculs,… (c’était un ordinateur HP 9830 à 4kHz avec 16 kb de mémoire). Comme ce « joueur » logiciel joue n’importe quoi de permis – pour faire l’anthropomorphisme la machine joue contre un idiot – , c’est un joueur bien faible aussi l’apprentissage est lent. On voit que la courbe d’apprentissage, (courbe A dans la fig.3) s’aplanit au fur et à mesure que le logiciel apprenant a pu éliminer des coups perdants et s’améliore. En effet l’ordinateur gagne plus en plus souvent avec de plus en d’expérience : sur la figure 3 on voit qu’entre la 100ème et la 2000eme partie, le logiciel apprenant n’a perdu qu’une cinquantaine de fois.

D’ailleurs, ce problème de la stratégie d’apprentissage est encore d’actualité. p. ex., Dennis & al. (2020) de l’University of California Berkeley discutent de stratégies d’apprentissage (par renforcement dans ce cas) qui mettent en oeuvre un agent (logiciel) antagoniste  « To [improve learning for] our protagonist agent, we introduce a second, antagonist agent » et ils nomment joliment leur technique «  Protagonist Antagonist Induced Regret Environment Design (PAIRED). » encourage le lecteur à aller vérifier dans l’article d’origine :  ici

Pour revenir à Talusumma, l’étudiant en 1975 proposait  « il faudrait terminer l’apprentissage en faisant jouer l’ordinateur contre un humain ». Mais qui aura la patience de faire des centaines de parties … car « pour faire perdre souvent la machine il faut constamment changer de tactique puisque la machine ne perd qu’une seule fois de la même manière. Il faudrait même parfois jouer un coup absurde espérant que parmi les possibilités de réponse, la machine choisisse la seule qui la fasse perdre et qu’elle n’a encore jamais joué. »

Fig 3: Victoires de algorithme apprenant protagoniste (N 1, en x) contre l’algorithme antagoniste (en y). Nombre  à atteindre 27. A, B, C illustrent trois stratégies : plus vite elle atteint l’horizontale, plus elle est efficace. [img]. Source : Lombard (1975)

Ou alors il faut de meilleures stratégies d’apprentissage automatiques. C’est ce qui avait été fait, avec les 2 autres stratégies illustrées dans la figure 3.

Trouver ces stratégies et peut-être de meilleures : un challenge pour vos élèves ?

Essayez de trouver les 2 autres stratégies illustrées dans la figure 3.  Peut-être en trouverez-vous des meilleures.
Après la publication d’où est tirée la figure 3 (Lombard, 1975), une 4ème méthode encore bien plus efficace (D non illustré) terminait son apprentissage avec certitude de ne plus faire d’erreurs en 134 parties -soit en 4-5 minutes plutôt qu’une nuit pour le générateur aléatoire (A).

Le code source en BASIC est aussi disponible (Faute de lecteur de bandes perforées et cassettes magnétiques, seul le listing papier est encore lisible de nos jours)

Remerciements