Le phénomène d’auto-siphonnage d’une chaine à billes ou de Newton

Fig 1: la chaîne sortant d’un bécher forme une arabesque très surprenante en « s’écoulant » d’un bécher : source Earth Unplugged
Une vidéo a retenu l’attention de nombreux internautes curieux de sciences : On y voit (cf. fig. 1) une chaînette à billes (comme celle qui retient une bonde de baignoire) s’élever – un peu comme un serpent – hors d’un bécher sur plusieurs centimètres avant de redescendre vers le sol. Le phénomène se maintient plusieurs secondes, jusqu’à vider le bécher. Le phénomène porte en anglais le très joli nom de chain fountain (fontaines de chaîne).
Cette vidéo étonnante peut susciter l’intérêt des élèves : elle met en défaut les modèles naïfs et les intuitions qui n’expliquent pas bien ce qui se passe. On peut l’employer afin de montrer la puissance explicative du modèle vectoriel pour comprendre ce phénomène.

Fig 2: la chaîne peut former un effet de fontaine en montant avant de descendre source Earth Unplugged
Steve Mould (cf. fig. 2) et cbsnews offrent une première explication de ce phénomène assez mystérieux : La chaine étant inextensible, sa vitesse est la même pour l’ensemble de sa longueur. Comme elle tombe rapidement, elle entraîne tout aussi rapidement les chaînons qui montent – au départ pour passer sur le rebord du bécher, mais le mouvement se poursuit et remonte même considérablement au-dessus du rebord. La vitesse de ces chaînons les empêche de changer de direction instantanément et ils continuent d’abord vers le haut avant de tourner et de plonger vers le sol. Cet équilibre dynamique produit ces magnifiques et surprenantes fontaines de chaîne « chain fountain ».
- Quelques lignes d’explication sur ce site de cbsnews
L’intuition suggère que chaque segment de la chaîne sortant du bécher est soumis à la traction de la partie de la chaine descendant vers le sol mais l’intuition perçoit difficilement l’inertie directionnelle qui l’empêche de changer de direction instantanément.
Pensé en termes de vecteur on voit mieux (ou on peut mieux faire voir…) que le vecteur vitesse ne peut pas varier très rapidement (le module est constant, mais la direction doit varier, cf. fig 3) et explique que chaque segment doive suivre cette belle courbe !

Fig 3: La modélisation en termes de vecteur,permet de comprendre que le changement de direction de la chaîne prend un temps non nul, parce que même à module constant le vecteur vitesse varie en direction. Cela explique en partie la courbure dynamique de la chaine. [img]
La puissance explicative du modèle vectoriel – en dissociant la vitesse linéaire de la chaine et sa direction – parait ici particulièrement manifeste.
La publication d’origine : c’est peut-être plus complexe …
Sur ce thème une publication récente dans Proceedings of the Royal Society A (Biggins, J. S., & Warner, M. (2014) présente une analyse plus approfondie et des mesures intéressantes.

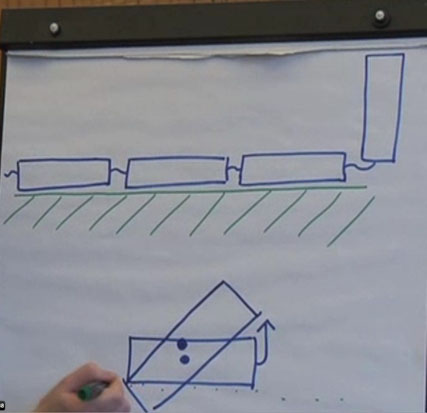
Fig 4: La chaine en se dépliant devrait s’enfoncer dans la surface de l’empilement à cause de son moment d’inertie, dont la rigidité produit une force de réaction. Modélisée comme un élément rigide, chaque maillon doit tourne et s' »appuie » sur le substrat produisant une réaction. source : Biggins, J. S., & Warner, M. (2014).
Ils montrent aussi que la hauteur atteinte par la boucle (h2) de la chaine est proportionnelle à la hauteur de chute h1. (Cf Fig 5)
Ils proposent que ce phénomène résulte aussi de l’action du moment cinétique produisant une force de réaction de la chaîne empilée dans le bécher : en effet en se dépliant la chaine – dont chaque chaînon est modélisé comme un segment rigide – produit une rotation de ces segments : en s’élevant d’un coté le segment devrait s’enfoncer dans la surface de la chaîne empilée dans le bécher qui offre une résistance d’où découle la réaction (cf fig. 4).
If a chain is initially at rest in a beaker at a height h1 above the ground, and the end of the chain is pulled over the rim of the beaker and down towards the ground and then released, the chain will spontaneously ‘flow’ out of the beaker under gravity. Furthermore, the beads do not simply drag over the edge of the beaker but form a fountain reaching a height h2 above it. We show that the formation of a fountain requires that the beads come into motion not only by being pulled upwards by the part of the chain immediately above the pile, but also by being pushed upwards by an anomalous reaction force from the pile of stationary chain. We propose possible origins for this force, argue that its magnitude will be proportional to the square of the chain velocity and predict and verify experimentally that h2∝h1. (Biggins, J. S., & Warner, M. (2014).
Biggins, J. S., l’un des auteur explique beaucoup plus en profondeur dans cette vidéo et montre les effets de varier la hauteur, le type de chaine, l’écart entre les chaînons.

Fig 5: La hauteur atteinte par la boucle (h2) de la chaine est proportionnelle à la hauteur de chute h1. Avec une chute de 10m h2 est impressionnante Source Biggins, J. S., & Warner, M. (2014).
Dans les perspectives, ils disent que leur résultat principal – que l’empilement offre une réaction lorsqu’une chaîne en est retirée – a des implications pour des processus industriels, dans le textile et la marine (Il faut se méfier lors du déroulement des chaines d’ancres), mais aussi le déploiement dans l’espace de structures ( minimiser l’énergie nécessaire).
Our central result — that when a chain is picked up from a pile the picking-up force is augmented by a reaction from the pile — may have consequences far beyond the chain fountain we study here. It will increase the rate at which any pile of chain is deployed when a force is applied at its end, and it will increase the energetic efficiency of the deployment process, which may have consequences for industrial design in areas as disparate as textiles and shipping. In areas such as space engineering (e.g. satellite tethers and space elevators) where efficiency is central, it may be worth maximizing the effect so that chain can be deployed with minimal expenditure of force and energy. (Biggins, J. S., & Warner, M. (2014).
Réagissez !!
Vous avez envie de réagir, de compléter, de préciser, de nuancer… La plateforme est faire pour cela vous pouvez commenter directement sur Expériment@l ou simplement répondre et je reporterai la réponse pour vous.
L’article original est ici :
-
Biggins, J. S., & Warner, M. (2014). Understanding the chain fountain. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 470(2163), 20130689. doi:10.1098/rspa.2013.0689 pdf depuis arxiv.og